[雑学] 下敷きの曲がりやすさの理論背景

目次
概要
工学・力学が得意なはるきちパパが,難しい式や専門用語を極力使わずに
下敷きの曲がりやすい方向についての解説をします.
立体駐車場の鉄骨の形にも通ずる話です.
ご興味あれば読んでください!
自由研究ネタにもどうぞ.
なんで育児ブログにこんな記事書いた?

いきなり意味わからんタイトルですね.
いやね,育児ブログって結構あるし,
うちのブログの特徴って何だろうって考えたんですね.
読書感覚な書き方したブログは結構あるし,
何か差別化できないかって考えたときに,
自分の得意な工学,力学分野の話をしようって思ったんです.
子供に「これなんでこうなるの?」って聞かれたときに,
ちゃんと理由を説明出来たらカッコいいし,子供の知識や好奇心も向上できますよね.
だから絶対プラスになるんです.
もちろん,数学や物理が苦手な人でも無理なくついてこれるように,
難しい専門用語や数式はできるだけ使わずに簡単にまとめますよ.
まずは騙されたと思って読んでみてください.
(2022/9/27 追記)
ただ知識蓄えるだけもなんかな~と思いまして,自由研究にも使えそうな内容に特化していこうかなと思いました.
現時点ではちょうど夏休みが終わったばかりですが,一年後にはある程度ネタが増えているかと思いますので,自由研究に困っている方は是非参考にしていただければ幸いです.
今回の問題設定
第一弾は下敷きの曲がりやすさの話です.
シチュエーションを想像してください.
子供が下敷きを曲げて遊んでいます.
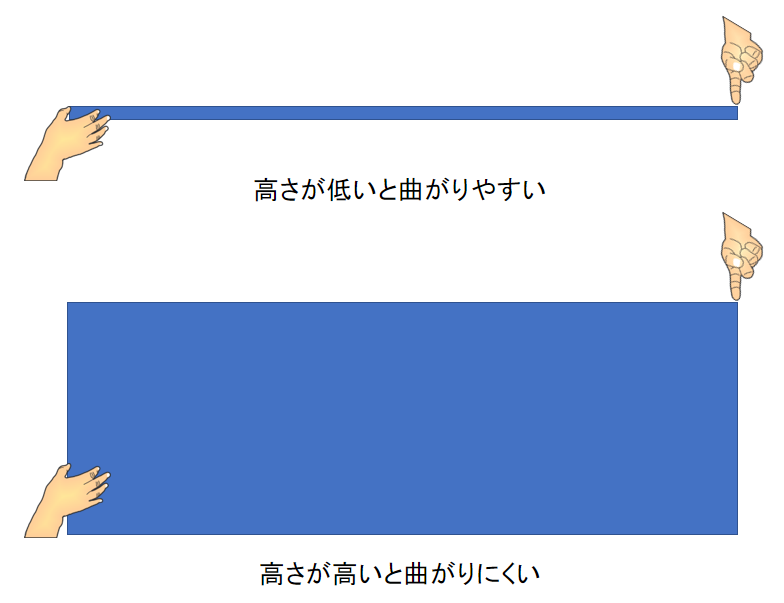
下敷きが地面と平行だと曲がりやすくて,
地面と垂直だと曲がりにくいことに気づきます.
(下の図を見てくだされ)
なんでだろう? と興味を持ちママパパに質問しました.
さて,その理由を紐解いていこうではありませんか.
「曲がる」現象に対して重要な項目とは?
まず,下敷きがどういう変形をするかを考えましょう.
「曲げて遊んでいます」の通り,曲がりますね.
ということで,「曲がる」という変形をする際の重要な項を見てみましょう.
数式を出したってしょうがないので,本当に重要な部分の抜粋です.
$$\frac{M}{E I}$$
こいつの値が大きいほど,より大きく曲がることを意味します.
Mはざっくり下敷きを折り曲げるときの力とでも思ってもらえればOKです.
分子に来ているので,力が大きければより曲がるってことですね.
Eは,材料の固さを表す数値が入ります.
例えばプラスチックより鉄のほうが固いよねって数値です.
Iは,物体の形状が持つ曲げ変形への耐性を表します.
ちょっと専門用語出しちゃいますが,Iは断面二次モーメントといいます.
まあ覚える必要はありませんが.
EとIは数値が大きいほど変形しにくいことを意味します.
どちらも分母に来ているので,より固いほど曲がりにくいってことですね.
こう聞くとイメージしやすいでしょ.
で,もともとの話としては,下敷きの向きが変わると変形のしやすさが変わるという話です.
繰り返しますが,Iは物体の形状が持つ曲げ変形のしにくさなので,
下敷きの向きによってIの値が変わります.
これがまさに下敷きが地面と平行か垂直かの違いなのです.
押す力が同じだとしたらMは一定ですし,
同じ下敷きならEは一定なので,
変わるのはIしかありません.
当たり前のことですが,式を見てみるとなんとなくわかった気になりますね.
I を詳しく見ていこう
では今度はIがどう決まるかを見ていきましょう.
まず,下敷きをズバッと切って断面形状を見てみましょう.
断面二次モーメントという名前だけあって断面が重要なんですね.
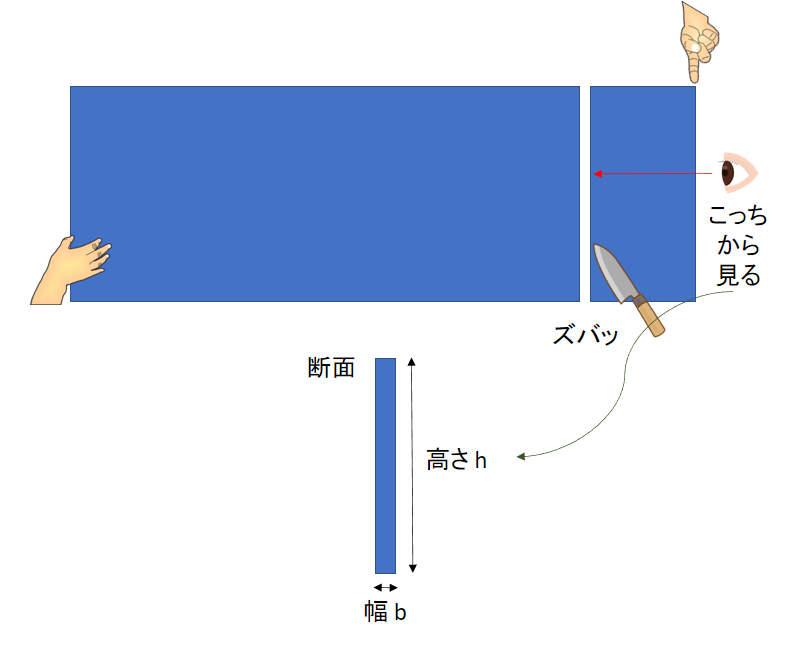
下敷きなので断面形状は四角形ですね.
四角形の断面二次モーメントは,公式により
$$I = \frac{b・{h^3}}{12}$$
で求まります.
ここで着目したいのは,高さであるhが三乗になっている点です.
つまり,幅が大きくなるより,高さが大きくなる方がメッチャ効くということです.
実際に計算してみましょう.
下敷きの厚さが1mm,辺の長さが100mmだとしましょう.
高さが低い,すなわち厚みが高さである場合のIは
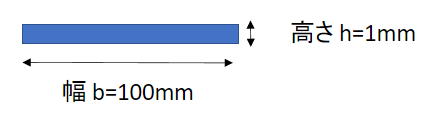
$$I = \frac{b・{h^3}}{12} = \frac{100・{1^3}}{12} = 8.333333$$
高さが低い,すなわち厚みが幅になる場合のIは
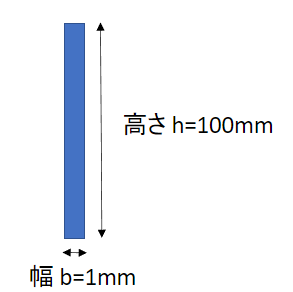
$$I = \frac{b・{h^3}}{12} = \frac{1・{100^3}}{12} = 83333.33$$
そう,実に一万倍変形しにくいのである.
高さが超大事なのわかったでしょうか?
もっとかみ砕いて言えば,押す力と同じ方向に部材が伸びてるから,
その分支える力が大きいとでも思えばいいと思います.
出たぞ鉄骨の話
ちなみに,高さが高いほど嬉しいというIの特性を活かした構造は世の中にたくさんあります.
例えばショッピングセンターの立体駐車場ってたくさんの鉄骨がありますよね.
その鉄骨の多くはアルファベットのIまたはHの形をしています.
高さを稼ぎたいけど真四角だと重くなっちゃうので,
中をくりぬいていくとこの形になるんですね.
まとめ

まとめると,曲げ変形で考慮すべきこととして
・曲げる力が大きいほど変形が大きい.
・材料の固さを示す指標があり数値が大きいほど変形が小さい.
・物体の形状による固さを示す指標があり数値が大きいほど変形が小さい.
・上二つは一定とすると形状による固さのみが影響し,それは高さが高いほど数値が大きくなる.
というところでしょうか.
まあこんな感じでまとめちゃったけど,
この記事の内容をそのまま伝えて理解してくれる子供は中高生以上かなぁ...
もっと小さい子供に教えるときは
・縦と横で何が変わったかな? → 高さが違うね.
・実は曲がるという動きには高さが大事なんだ. → 高いほど曲がりにくいんだよ.
・高いほど押す力と同じ方向に下敷きが伸びてるから,より支えられるんだよ.
って感じですかねぇ.
最終的に言いたいこと最初から皆さんわかっていたと思いますが,
こうやって理論を知るとまた違う見方もできるし興味がわいてきますよね.
まさに親子両方とも成長できるのです.
最後のご挨拶
第一弾はこんな感じかな.
わかりやすく書けてたでしょうか?
工学・力学の話に限らず,
意外とためになる雑学についてたま~に書いていこうと思います.
知りたいこととかあったら是非連絡してくださいね😉
特に調べ方すらわからん問題の時は役に立つかもです笑
難しいことは書かずにできるだけわかりやすく書きますよ.
SNSもやっているので,よかったらフォローお願いします♪
ツイッター: @harukichipapaik
インスタ: harukichi_papaik
それでは最後までお読みいただきありがとうございました!









ディスカッション
コメント一覧
まだ、コメントがありません